选择排序

简介：

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。
首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

算法描述：

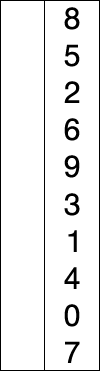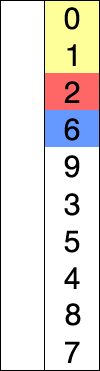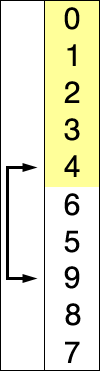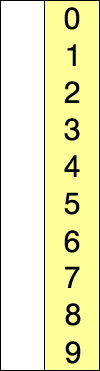
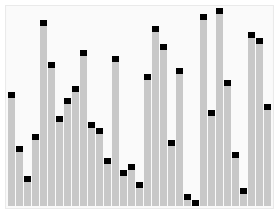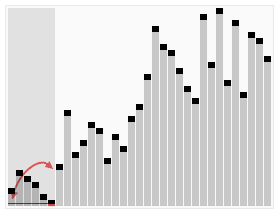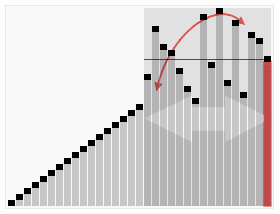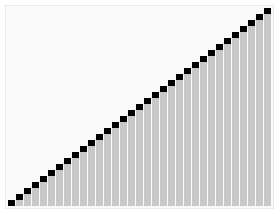
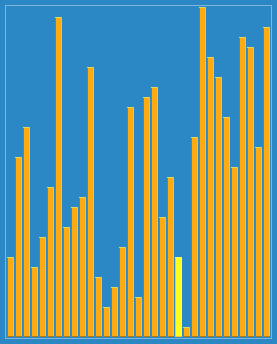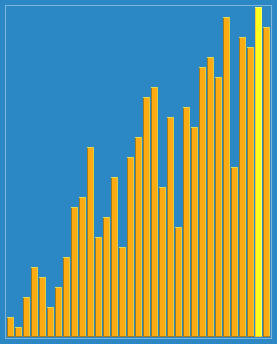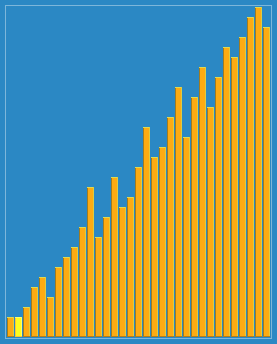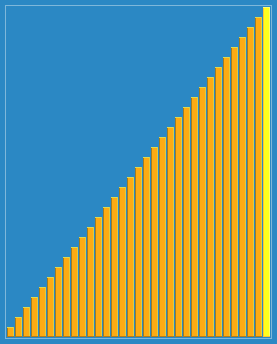
选择排序的示例动画。红色表示当前最小值，黄色表示已排序序列，蓝色表示当前位置

直接选择排序(Straight Select Sorting) 又称简单选择排序，其实现方法是：
第一趟从n个无序记录中找出最小的记录与第一个记录交换(此时第一个记录看为有序)；
第二趟从第二个记录开始的n-1个无序记录中再选出关键字最小的记录与第二个记录交换(此时，第一个和第二个记录为有序)……
如此下去，第i趟从i个记录开始的n-i+1个无序记录中选出关键字最小的记录与第i个记录交换(此时，前i个记录已有序)，
此时n-1趟后前n-1个记录已有序，无序记录只剩一个即第n个记录．因关键字小的前n-1个记录已进入有序序列，这第n个记录必为关键字最大的记录．
所以，无需再交换，n个记录已全部有序．

选择排序视频演示　
 备份链接1

过程演示：

首先：
       a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
　　　　 3     0     1     8     7     2     5     4     9     6
　　　　 
       //首先，拿出a[0],作为有序有序，当其为最小值，并依次比较，若大于则交换．
　　　　 3     0     1     8     7     2     5     4     9     6
       //　a[0] = 3, 和a[1]比较，交换，
　　　　[0]    3     1     8     7     2     5     4     9     6   
       //　a[0] = 0 ,继续和a[2] ,a[3] ...比较
　　　　[0]    3     1     8     7     2     5     4     9     6       
       //　拿出a[１] = 3 ,和a[2] ,a[3] ...比较
　　　　[0]    1     3     8     7     2     5     4     9     6       
       //　拿出a[１] = 1 ,和a[3] ,a[4] ...比较
　　　　[0     1]    3     8     7     2     5     4     9     6   　　　　
       //　拿出a[2] = 3 ,和a[3] ,a[4] ...比较
　　　　[0     1]    3     8     7     2     5     4     9     6  
       //　拿出a[2] = 3 ,和a[5] 比较时，大于，交换
　　　　[0     1]    2     8     7     3     5     4     9     6 
       //　拿出a[3] = 8 ,和a[4] ,a[5] ...比较
　　　　[0     1     2]    8     7     3     5     4     9     6  　　　　 
       //　拿出a[3] = 8 ,和a[5] = 3 比较时，大于，交换
　　　　[0     1     2]    3     7     8     5     4     9     6 
       //　拿出a[3] = 3 ,和a[6] ,a[7]... 比较
　　　　[0     1     2     3]    7     8     5     4     9     6 
       //　拿出a[4] = 7 ,和a[5] ,a[6]... 比较
　　　　[0     1     2     3]    7     8     5     4     9     6 
       //　拿出a[4] = 7 ,和a[6] = 5 比较时，大于，交换
　　　　[0     1     2     3]    5     8     7     4     9     6 
       //　拿出a[4] = 5 ,和a[7] = 4 比较时，大于，交换
　　　　[0     1     2     3]    4     8     7     5     9     6 
       //　拿出a[4] = 4 ,和a[8] ,a[9]...比较
　　　　[0     1     2     3]    4     8     7     5     9     6 
       //　拿出a[4] = 4 ,和a[8] ,a[9]...比较,得：
　　　　[0     1     2     3     4]    8     7     5     9     6 
       //　拿出a[5] = 8 ,和a[6] ,a[7]...比较
　　　　[0     1     2     3     4]    8     7     5     9     6 
       //　拿出a[5] = 8 ,和a[6] = 7 比较时，大于，交换
　　　　[0     1     2     3     4]    7     8     5     9     6 
       //　拿出a[5] = 7 ,和a[7] = 5 比较时，大于，交换
　　　　[0     1     2     3     4]    5     8     7     9     6 
       //　拿出a[5] = 5 ,和a[8],a[9] 比较,
　　　　[0     1     2     3     4]    5     8     7     9     6 
       //　拿出a[5] = 5 , 比较完后得：
　　　　[0     1     2     3     4     5]    8     7     9     6 
       //　拿出a[6] = 8 , 和a[7] ,a[8]...比较
　　　　[0     1     2     3     4     5]    8     7     9     6 　
       //　拿出a[6] = 8 , 和a[7]　= 7 比较时，大于，交换
　　　　[0     1     2     3     4     5]    7     8     9     6 　
       //　拿出a[6] = 7 , 和a[8],a[9]...比较
　　　　[0     1     2     3     4     5]    7     8     9     6 　
       //　拿出a[6] = 7 , 和a[9] = 6 比较时，大于，交换
　　　　[0     1     2     3     4     5]    6     8     9     7 　
       //　拿出a[6] = 7 , 比较时，大于，交换之后得：
　　　　[0     1     2     3     4     5     6]    8     9     7 
       //　拿出a[7] = 8 , 和a[8],a[9] 比较:
　　　　[0     1     2     3     4     5     6]    8     9     7 
       //　拿出a[7] = 8 , 和a[9] = 7  比较,比较时，大于，交换，　得:
　　　　[0     1     2     3     4     5     6]    7     9     8 　　
       //　拿出a[7] = 7 , 和a[8],a[9] 比较:
　　　　[0     1     2     3     4     5     6     7     9     8 　　　 　　    
       //　拿出a[7] = 8 , 比较时，大于，交换之后得：
　　　　[0     1     2     3     4     5     6     7]    9     8 　
       //　拿出a[8] = 9 , 和a[9] = 8 比较,比较时，大于，交换之后得：
　　　　[0     1     2     3     4     5     6     7     8]    9 
       //　拿出a[9] = 9 , 可得：
　　　　[0     1     2     3     4     5     6     7     8]    9 


　　　　我们可以看到，通过每次在序列中找到最小的值放到有序中，依次排列下去，即可完成排序过程．

时间复杂度：

选择排序的交换操作介于 0 和 (n - 1） 次之间。
选择排序的比较操作为 n (n - 1） / 2次之间。
选择排序的赋值操作*介于0和3 ＊(n - 1） 次之间。
比较次数O(n^2），比较次数与关键字的初始状态无关，总的比较次数`N=(n-1）+(n-2）+…+1=n(n-1）/2。交换次数O(n），最好情况是，已经有序，交换0次；最坏情况交换n-1次，逆序交换n/2`次。
交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

稳定性：

选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。
那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。
比较拗口，举个例子，比如序列[5， 5， 3]第一次就将第一个[5]与[3]交换，导致第一个5挪动到第二个5后面。所以选择排序是一个不稳定的排序算法。

程序代码：

按照此定义，我们很容易写出选择排序的程序代码：

int Select_Sort(int *a, int size)
{
    if(NULL == a)
    {
        return -1;
    }
    int i = 0;
    int j = 0;
    int tmp = 0;
    for(i =　0; i < size; ++i)
    {
        for(j = i　+　1; j　< size; ++j)
        {
            if(a[j] < a[i])
            {
                tmp = a[j];
                a[j]= a[i];
                a[i] = tmp;
            }
        }
    }
    return 0;
}

功能检测

检测代码：

int main()
{
    int i =0;
    int a[] = {3,0,1,8,7,2,5,4,6,9};
    int n = sizeof(a)/sizeof(a[0]);

    Select_Sort(a, n);

    printf("\n");
    for(i = 0; i < n ; ++i)
    {
        printf("%3d",a[i]);
    }
    printf("\n");
    return 0;
}

运行结果：

root@aemonair:~/Desktop# cc.sh Select_Sort.c 
Compiling ...
-e CC      Select_Sort.c -g -lpthread
-e         Completed .
-e         Fri Jul 29 10:48:44 CST 2016
root@aemonair:~/Desktop# ./Select_Sort

  0  1  2  3  4  5  6  7  8  9

总结：

在直接选择排序中，共需要进行n-1次选择和交换，每次选择需要进行n-i次比较 (1<=i<=n-1),而每次交换最多需要3次移动，因此，总的比较次数C=(n*n - n)/2,
总的移动次数3(n-1).由此可知，直接选择排序的时间复杂度为O(n2) (n的平方)，所以当记录占用字节数较多时，通常比直接插入排序的执行速度快些。
由于在直接选择排序中存在着不相邻元素之间的互换，因此，直接选择排序是一种不稳定的排序方法。

原地操作几乎是选择排序的唯一优点，当方度（space complexity）要求较高时，可以考虑选择排序；实际适用的场合非常罕见。

文章作者: Air

文章链接: http://aemonair.github.io/2016/07/29/Sort_5_SelectionSort/

DataStruct Sort