排序_4.希尔排序

希尔排序

简介：

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
• 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

算法描述：

假设有一个很小的数据在一个已按升序排好序的数组的末端。
如果用复杂度为O(n2)的排序（冒泡排序或插入排序），可能会进行n次的比较和交换才能将该数据移至正确位置。
而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置。

希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。
这样可以让一个元素可以一次性地朝最终位置前进一大步。
然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

• 该方法的基本思想是：
  先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。
  因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率上有较大提高。

• 一个更好理解的希尔排序实现：
  将数组列在一个表中并对列排序（用插入排序）。
  重复这过程，不过每次用更长的列来进行。
  最后整个表就只有一列了。
  将数组转换至表是为了更好地理解这算法，算法本身仅仅对原数组进行排序（通过增加索引的步长，例如是用i += step_size而不是i++）。

希尔排序视频演示　
备份链接１　

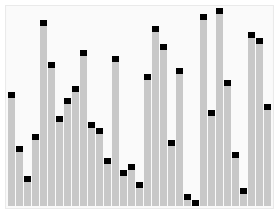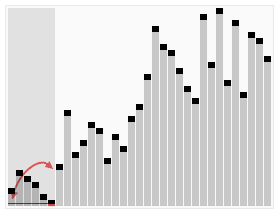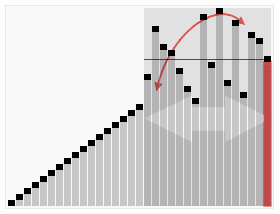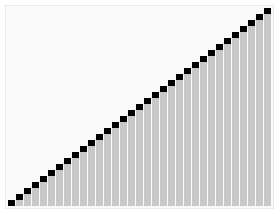
过程演示：

首先：
       a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
　　　　 3     0     1     8     7     2     5     4     9     6
　　　　 // 首先．步长= 个数/2 ＝　１０／２　＝　５，
　　　　 //所以，a[0]和a[5]比较，a[1]和a[6]比较...如果大于就交换．
 ->     3     0     1     8     7     2     5     4     9     6
        |     |     |     |     |     |     |     |     |     |
        3     |     |     |     |     2     |     |     |     |
        2     |     |     |     |     3     |     |     |     |
              0     |     |     |           5     |     |     | 
                    |     |     |                 |     |     |
                    1     |     |                 4     |     |
                          8     |                       9     |
                                |                             |
                                7                             6
                                6                             7
	   // 步长为5时，两两比较做交换之后，得到：
	   //(视频中，下一次步长为３，如下)，所以，a[0]和a[3]比较，a[1]和a[4]比较...如果大于就交换．
      a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
->      2     0     1     8     6     3     5     4     9     7
        |     |     |     |     |     |     |     |     |     |
        2     |     |     8     |     |     5     |     |     7
              |     |           |     |           |     |
              0     |           6     |           4     |
                    1                 3                 9
       2        <         8
              0       <         6
                    1        <        3  
                          8        >        5     //swap
    		              5                 8
       2        <         5        <        8     
                                6        >        4   //swap
              0        <        4        <        6
                                      3        <        9
                                            8        >        7  //swap
                          5         <       7        <        8
       //经过步长为３的比较及交换，我们得到如下序列：
	   //(下一次步长为１，如下)，所以，a[0]和a[1]比较，a[1]和a[2]比较...如果大于就交换．
      a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
->     2     0     1     5     4     3     7     6     9     8
       2  >  0  //swap
       0  <  2
             2  >  1
             1  <  2
                   2  <  5
                         5  >  4
                         4  <  5
                               5  >  3
                               3  <  5 
                         4  >  3 
                         3  <  4 
                   2  <  3  <  4
                                     5  <  7
                                           7  >  6
                                           6  <  7
                                                       9
                                                       9  >  8
                                                       8  <  9
	   //此时比较交换都已经完成，得到有序序列．
      a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]                                           
       0     1     2     3     4     5     6     7     8     9


	　//(实际中，下一次步长可以为5/2 = 2，如下)，所以，a[0]和a[2]比较，a[1]和a[3]比较...如果大于就交换．
      a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
->	   2     0     1     8     6     3     5     4     9     7
       |     |     |     |     |     |     |     |     |     |
       2     |     1     |     6     |     5     |     9     |
             |           |           |           |           |
             0 	         8           3	         4	         7
       1	       2    //小于，向后
       1	       2	       6	       5　　//小于，向后，大于，交换
       1	       2	       5	       6
       1	       2	       5	       6	       9  //小于，向后
       
        //得到的一个２步长序列
=      1           2           5           6           9

             0           8　　//小于，向后
             0           3           8　　　//小于，向后
             0           3           4           8　　　//小于，向后，大于，交换
=            0           3           4           7           8

      //(下一次步长为2/2 = １，如下)，所以，a[0]和a[1]比较，a[1]和a[2]比较...如果大于就交换．
      a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
>      1     0     2     3     5     4     6     7     9     8
       1     0
       0     1
       0     1     2
       0     1     2     3 
       0     1     2     3     5
       0     1     2     3     5     4
       0     1     2     3     4     5
       0     1     2     3     4     5     6
       0     1     2     3     4     5     6     7
       0     1     2     3     4     5     6     7     9
       0     1     2     3     4     5     6     7     8     9
	  //得到有序序列：
      a[0]  a[1]  a[2]  a[3]  a[4]  a[5]  a[6]  a[7]  a[8]  a[9]
       0     1     2     3     4     5     6     7     8     9

　　　　我们可以看到，分成若干序列的各部分，通过缩减增量的分别排序，使得分别有序，再进行插入排序时，因为插入排序对元素基本有序的效率高，使得希尔排序效率很高．

　　　　

程序代码：

按照此定义，我们可以写出希尔排序的程序代码：

int shell_sort(int *a, int size)
{
    if(NULL == a)
    {
        return -1;
    }
    int i = 0;
    int j = 0;
    int tmp =0;
    int inc = size/2;
    while(inc > 0)
    {
        for(i = 0; i+inc < size; ++i)
        {
            if(a[i] > a[i+inc])
            {
                tmp = a[i];
                a[i] = a[i+inc];
                a[i+inc] = tmp;
                j=i;
                while((a[j] < a[j-inc]) && (j-inc)>=0)
                {
                        tmp = a[j];
                        a[j] = a[j-inc];
                        a[j-inc] = tmp;
                        j-=inc;
                }
            }
        }

        inc/=2;
    }
    return 0;
}

void shellsort1(int a[], int n)
{
    int i   = 0 ;
    int j   = 0 ; 
    int gap = 0 ;
    for (gap = n / 2; gap > 0; gap /= 2) //步长
    {
        for (i = 0; i < gap; i++)//按组排序
        {
            for (j = i + gap; j < n; j += gap)
            {
                if (a[j] < a[j - gap])
                {
                    int temp = a[j];
                    int k = j - gap;
                    while (k >= 0 && a[k] > temp)
                    {
                        a[k + gap] = a[k];
                        k -= gap;
                    }
                    a[k + gap] = temp;
                }
            }
        }
    }
}

这样的代码量太大，于是每次从数组第gap个元素开始,每个元素与自己组内的数据进行直接插入排序。

void shellsort2(int a[], int n)
{
        int j   = 0 ;
        int gap = 0 ;
        for (gap = n / 2; gap > 0; gap /= 2)
        {
            for (j = gap; j < n; j++)// 从数组第gap个元素开始
            {
                if (a[j] < a[j - gap]) // 每个元素与自己组内的数据进行直接插入排序
                {
                    int temp = a[j];
                    int k = j - gap;
                    while (k >= 0 && a[k] > temp)
                    {
                        a[k + gap] = a[k];
                        k -= gap;
                    }
                    a[k + gap] = temp;
                }
            }
        }
}

void shellsort3(int a[], int n)
{
    int   i = 0 ;
    int   j = 0 ; 
    int gap = 0 ;
    int tmp = 0 ;
    for(gap = n / 2; gap > 0; gap /= 2)
    {
        for(i = gap; i < n; i++)
        {
            for(j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap)
            {
                tmp = a[j];
                a[j] = a[j+gap];
                a[j+gap] = tmp;
            }
        }
    }
}

功能检测

• 检测代码：

  int main()
  {
      int i =0;
      int a[] = {23,3,44,2,11,33,21,43,54,67};
                  //{3, 0, 1, 8, 7, 2, 5, 4, 9, 6};
      int n = sizeof(a)/sizeof(a[0]);
  
  //    shell_sort(a, n);
  //    shellsort1(a, n);
  //    shellsort2(a, n);
      shellsort3(a, n);
      printf("\n");
      for(i = 0; i < n ; ++i)
      {
          printf("%3d",a[i]);
      }
      printf("\n");
      return 0;
  }

• 运行结果：

root@aemonair:~/Desktop# make Shell_Sort
cc     Shell_Sort.c   -o Shell_Sort
root@aemonair:~/Desktop# ./Shell_Sort

  2  3 11 21 23 33 43 44 54 67

步长序列

步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，最终算法以步长为1进行排序。当步长为1时，算法变为插入排序，这就保证了数据一定会被排序。

Donald Shell最初建议步长选择为 n/2并且对步长取半直到步长达到1。虽然这样取可以比 O(n^2) 类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的。比如，如果一个数列以步长5进行了排序然后再以步长3进行排序，那么该数列不仅是以步长3有序，而且是以步长5有序。如果不是这样，那么算法在迭代过程中会打乱以前的顺序，那就不会以如此短的时间完成排序了。

已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,...)，该序列的项来自[9* (4^i)]-[9* (2^i)]+1和和 2^(i+2) * [2^(i+2)-3]+1这两个算式.[1]
这项研究也表明“比较在希尔排序中是最主要的操作，而不是交换。”用这样步长序列的希尔排序比插入排序要快，甚至在小数组中比快速排序和堆排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

另一个在大数组中表现优异的步长序列是（斐波那契数列除去0和1将剩余的数以黄金分区比的两倍的幂进行运算得到的数列）：(1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713,…)[2]

---

引用

希尔排序－维基百科
白话经典算法系列之三 希尔排序的实现