插入排序
简介:
所谓插入排序,就是把一个记录按其关键字的大小插入到一个有序的记录序列中,插入后该序列依然有序.
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。

算法描述:
将记录集合分为有序和无序两个序列.
从无序序列中任取一个元素,然后根据该元素的记录关键字大小在有序序列中找到一个合适的位置which 使得该记录放入这个位置后,这个有序序列依然保持有序.
每插入一个记录就称为一趟插入排序,经过多趟插入排序,使得该无序序列中的记录全部插入到有序序列中,则排序完成.
- 直接插入排序(straight insertion sort)的做法是:
- 每次从无序表中取出第一个元素,把它插入到有序表的合适位置,使有序表仍然有序。
- 第一趟比较前两个数,然后把第二个数按大小插入到有序表中;
- 第二趟把第三个数据与前两个数从后向前扫描,把第三个数按大小插入到有序表中;
- 依次进行下去,进行了(n-1)趟扫描以后就完成了整个排序过程。
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5


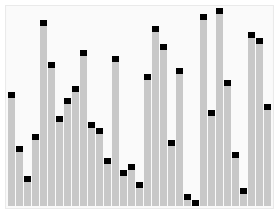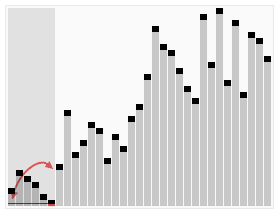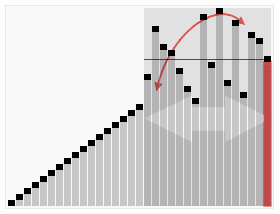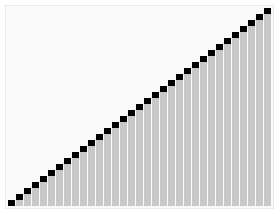
过程演示:
插入排序视频演示
备份链接1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| 首先:
a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9]
3 0 1 8 7 2 5 4 9 6
- 第一次:
// 认为3是有序序列,取出下一个0和其比较,插入(这里化简了插入过程,即计较当前值和有序序列,大的都向后移动...)
[0 3] 1 8 7 2 5 4 9 6
// [0 3]是有序序列,取出下一个1和其比较,插入
[0 1 3] 8 7 2 5 4 9 6
// [0 1 3]是有序序列,取出下一个8和其比较,插入
[0 1 3 8] 7 2 5 4 9 6
// [0 1 3 8]是有序序列,取出下一个7和其比较,插入
[0 1 3 7 8] 2 5 4 9 6
// [0 1 3 7 8]是有序序列,取出下一个2和其比较,插入
[0 1 2 3 7 8] 5 4 9 6
// [0 1 2 3 7 8]是有序序列,取出下一个5和其比较,插入
[0 1 2 3 5 7 8] 4 9 6
// [0 1 2 3 5 7 8]是有序序列,取出下一个4和其比较,插入
[0 1 2 3 4 5 7 8] 9 6
// [0 1 2 3 4 5 7 8]是有序序列,取出下一个9和其比较,插入
[0 1 2 3 4 5 7 8 9] 6
// [0 1 2 3 5 7 8 9]是有序序列,取出下一个6和其比较,插入
[0 1 2 3 4 5 6 7 8 9]
这时,我们看到一直有两组区域,一组有序区域,一组无序的区域,在无序区域内找一个数,插入到有序区域中,即可获得有序序列。
|
程序代码:
按照此定义,我们很容易写出插入排序的程序代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void insert_sort(int *a, int size)
{
int i = 0;
int j = 0;
int temp =0;
for(i = 0; i < size; ++i)
{
for(j = i+1; (a[j] < a[j-1] && j > 0); --j)
{
temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void insert_sort1(int *array, int length)
{
int i = 0;
int j = 0;
for(i = 0; i < length - 1; ++i)
{
for(j = i + 1; j < length; ++j)
{
//只要array[i]比array[j]大就交换,这样每次遍历一边我们得到当前最小值.i++的时候向后放.
if(array[i] > array[j])
{
//swap(&array[i], &array[j], sizeof(int));
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void insert_sort2(int *array, int length)
{
int i = 0;
int j = 0;
int key = 0;
for(i = 1; i < length; ++i)
{
key = array[i]; // key = array[i]
for(j = i - 1; j >= 0 && array[j] > key; --j) // 若array[j]>key 将所有元素向后移
{
array[j + 1] = array[j];
}
array[j + 1] = key; // 直到不比它大,将key设到array[j+1]
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void insert_sort3(int *array, int length)
{
int i = 0;
int j = 0;
int temp = 0;
for(i = 1; i < length; ++i)
{
for(j = i - 1; j >= 0 && array[j] > array[j + 1]; --j)
{
temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
//swap(&array[j], &array[j + 1], sizeof(array[0]));
}
}
}
|
这里的插入排序都需要做很多次比较,再进行插入.
如果,数据量特别大的时候,比较的情况也会浪费很多时间.
如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找插入排序。
复杂度
如果目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。
最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。
最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上(n-1)次。
平均来说插入排序算法复杂度为O(n2)。
因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。
插入排序在工业级库中也有着广泛的应用,在STL的sort算法和stdlib的qsort算法中,都将插入排序作为快速排序的补充,用于少量元素的排序(通常为8个或以下)。
稳定性
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。
比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
功能检测
- 检测代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int main()
{
int i =0;
int a[] = {2,1,5,6,3,9,-1,7};
int n = sizeof(a)/sizeof(a[0]);
insert_sort1(a, n);
printf("\n");
for(i = 0; i < n ; ++i)
{
printf("%3d",a[i]);
}
printf("\n");
return 0;
}
|
- 运行结果:
1
2
3
4
5
6
7
8
| root@aemonair:~/Desktop# cc.sh Insert_Sort.c
Compiling ...
-e CC Insert_Sort.c -g -lpthread
-e Completed .
-e Wed Jul 27 19:45:54 CST 2016
root@aemonair:~/Desktop# ./Insert_Sort
-1 1 2 3 5 6 7 9
|
总结
插入排序不适合对于数据量比较大的排序应用。
但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。