快速排序
简介:
快速排序(
QuickSort)是对冒泡排序的一种改进的交换排序算法,又称 分区交换排序(partition-exchange sort).
在平均状况下,快速排序排序n个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。
事实上,快速排序通常明显比其他Ο(n log n)算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。因此称为快速排序.
算法描述:
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
- 步骤为:
从数列中挑出一个元素,称为”基准”(pivot),
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
- 化简得:
- 先从数列中取出一个数作为基准数。
- 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
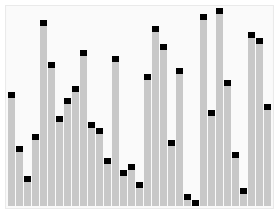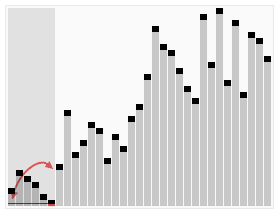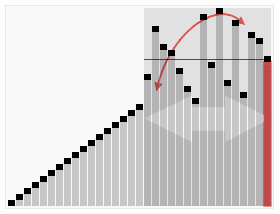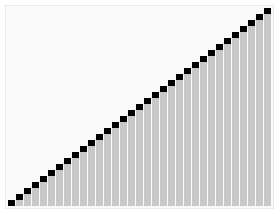
过程演示:
1 | |
程序代码:
// 快排思路:
//
// 1,选取一个数值为关键值并且记录下来
// 2. 给定两个下标i,j分别指向头和尾(0, length - 1)
//
// 3.循环操作:
// 从后向前找遇到比关键值小的放在i下标;
// 从前向后找遇到比关键值大的放在j下标;
// 当i和j相等,退出
// 把关键值填充进去
//
// 4.对关键值两边做递归处理
按照此定义,我们很容易写出快速排序的程序代码:
1 | |
算法Partition完成在给定区间s[i]~s[j]中,一趟快速排序的划分.
1.设置两个搜索指针i和j来指向给定区间的第一个和最后一个记录,并将第一个作为基准.
2.首先,从j指针开始向左搜索比基准小的记录(即,该记录应该位于基准的左侧),找到后将其交换到i指针处(此时位于基准的左侧);
3.i指针右移一个位置,由此开始自左向右搜索比基准大的记录(即,该记录应该位于基准的右侧);
4.j指针左移一个位置,并继续上述自右向左搜索,交换的过程.
5.如此由两端交替向中间搜索交换,直到i,j相等,表明,i记录的左侧都比基准小,j右侧都比基准值大.而i,j指向的同一个位置,就是基准值最终要放置的位置.
对其合并整理,优化代码如下:
1 | |
1 | |
算法分析



功能检测
- 检测代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16int main()
{
int i =0;
int a[] = {3,0,1,8,7,2,5,4,6,9};
int n = sizeof(a)/sizeof(a[0]);
quicksort1(a, 0, n-1);
// QuickSort2(a, 0, n-1);
printf("\n");
for(i = 0; i < n ; ++i)
{
printf("%3d",a[i]);
}
printf("\n");
return 0;
} - 运行结果:
1 | |
总结:
快速排序被认为是在所有同数量级(O(n lg n))的排序算法中平均性能最好.
但是如果初始序列有序或基本有序时,快速排序将退化成冒泡排序,此时的时间复杂度上升到O(n^2).
对此我们有如下优化方案:
如以中间的数作为基准数的,or随机选择基准数,and区间内数据较少时直接用另的方法排序以减小递归深度。
三平均分区法
关于这一改进的最简单的描述大概是这样的:与一般的快速排序方法不同,它并不是选择待排数组的第一个数作为基准,而是选用待排数组最左边、最右边和最中间的三个元素的中间值作为基准。这一改进对于原来的快速排序算法来说,主要有两点优势:
(1) 首先,它使得最坏情况发生的几率减小了。
(2) 其次,未改进的快速排序算法为了防止比较时数组越界,在最后要设置一个哨点。根据分区大小调整算法
这一方面的改进是针对快速排序算法的弱点进行的。快速排序对于小规模的数据集性能不是很好。可能有人认为可以忽略这个缺点不计,因为大多数排序都只要考虑大规模的适应性就行了。但是快速排序算法使用了分治技术,最终来说大的数据集都要分为小的数据集来进行处理。
由此可以得到的改进就是,当数据集较小时,不必继续递归调用快速排序算法,而改为调用其他的对于小规模数据集处理能力较强的排序算法来完成.
另一种快速排序的改进策略是在递归排序子分区的时候,总是选择优先排序那个最小的分区。这个选择能够更加有效的利用存储空间从而从整体上加速算法的执行。