冒泡排序
简介:
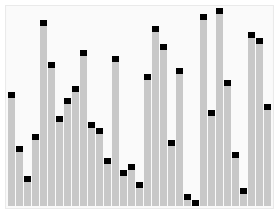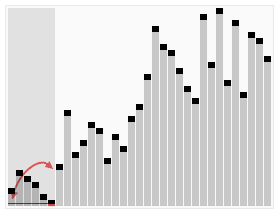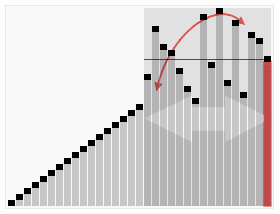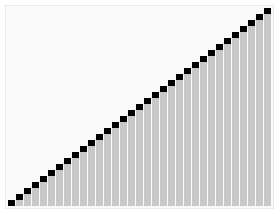
冒泡排序(BubbleSort)是一种流行的排序算法,这个排序过程就像一个个向上(向右)冒泡的气泡,最轻的气泡先冒上来(到达R[n]位置),较重的气泡后冒上来,因此形象的称之为冒泡排序.

第一趟从第一个记录R[1]开始到第n个记录R[n]为止,对(n- 1个对)相邻的两个记录进行比较,若与排序要求相逆,则交换两者的位置.
这样,经过一趟的比较,交換後,具有最大关键值的记录就会被交换到R[n]位置.
第二趟从第一个记录R[1]开始到n - 1个记录R[n-1]为止继续重复上述的比较与交换,这样具有次大关键字的记录就被交换到R[n-1]位置.
如此重复,在经过n - 1 趟这样的比较与交换之后,R[1]~R[n]这n个记录已按关键字有序.
设数组长度为N。
1. 比较相邻的前后二个数据,如果前面数据大于后面的数据,就将二个数据交换。
2. 这样对数组的第0个数据到N-1个数据进行一次遍历后,最大的一个数据就“沉”到数组第N-1个位置。
3. N=N-1,如果N不为0就重复前面二步,否则排序完成。
冒泡排序视频演示
备份链接1
过程演示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| 首先:
a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9]
3 0 1 8 7 2 5 4 6 9
第一步:
//a[0] 比较 a[1] , 3 <---> 0,大,交换,得:
0 3 1 8 7 2 5 4 6 9
//a[1] 比较 a[2] , 3<--->1,大,交换,得:
0 1 3 8 7 2 5 4 6 9
//a[2] 比较 a[3] , 3<---> 8,小,不变,得:
0 1 3 8 7 2 5 4 6 9
//a[3] 比较 a[4] , 8<---> 7,大,交换,得:
0 1 3 7 8 2 5 4 6 9
//a[4] 比较 a[5] , 8<---> 2,大,交换,得:
0 1 3 7 2 8 5 4 6 9
//a[5] 比较 a[6] , 8<---> 5,大,交换,得:
0 1 3 7 2 5 8 4 6 9
//a[6] 比较 a[7] , 8<---> 4,大,交换,得:
0 1 3 7 2 5 4 8 6 9
//a[7] 比较 a[8] , 8<---> 6,大,交换,得:
0 1 3 7 2 5 4 6 8 9
//a[8] 比较 a[9] , 8<---> 9,小,不变,得:
0 1 3 7 2 5 4 6 8 9
这时,经过一次遍历,我们得到了最大值已经被冒(放置)在最右边,接下来,重复这样的操作,到n-1的位置,得到次大.
第二次:
a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9]
0 1 3 7 2 5 4 6 8 9
//a[0] 比较 a[1] , 0 <---> 3,小,不变,得:
0 1 3 7 2 5 4 6 8 9
//a[1] 比较 a[2] , 1 <---> 3,小,不变,得:
0 1 3 7 2 5 4 6 8 9
//a[2] 比较 a[3] , 3 <---> 7,小,不变,得:
0 1 3 7 2 5 4 6 8 9
//a[3] 比较 a[4] , 7 <---> 2,大,交换,得:
0 1 3 2 7 5 4 6 8 9
//a[4] 比较 a[5] , 7 <---> 5,大,交换,得:
0 1 3 2 5 7 4 6 8 9
//a[5] 比较 a[6] , 7 <---> 4,大,交换,得:
0 1 3 2 5 4 7 6 8 9
//a[6] 比较 a[7] , 7 <---> 6,大,交换,得:
0 1 3 2 5 4 6 7 8 9
//a[7] 比较 a[8] , 7 <---> 8,小,不变,得:
0 1 3 2 5 4 6 7 8 9
...
我们可以看到,通过第二次,我们得到了次大元素并放入右边倒数第二个位置上,我们若继续重复,通过得到剩余元素中最大值,可以得到整个元素组里大小排列出来的次序.即可完成排序过程.
|
程序代码:
按照此定义,我们很容易写出冒泡排序的程序代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| void BubbleSort1(int *a, int size)
{
if(NULL == a || size < 0)
{
return;
}
int i = 0 ;
int j = 0 ;
int n = size;
for(i = 0; i < n; i++)
{
for(j = 1; j < n - i; j++)
{
if(a[j-1] > a[j])
{
Swap(&a[j-1], &a[j]);
}
}
}
}
|
即是将元素依次比较,若反序则交换.
我们可以看出,这样的流程会有很多重复.那么我们该怎么样进行优化呢?
如果是一个已经排好序的序列使用上述的方案进行排序的话,则在第一次的循环中则不会出现交换的过程(因为前一个数据的值总是小于后一个数据),所以我们以是否发生了交换作为排序是否结束的标志。及如果一轮排序中并没有发生交换过程则说明当前的序列是已序的。
0 1 2 3 5 8 9 4 6 7
比如这个序列,基本有序,当我们排好后面的元素后,前面已经排好序,那么我们就可以少进行比较.
我们可以设置一个标志,如果这一趟发生了交换,则为true,否则为false。如果明显如果有一趟没有发生交换,说明排序已经完成。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #define TRUE 1
#define FALSE 0
typedef unsigned char Boolean;
void BubbleSort2(int *a, int size)
{
if(NULL == a || size < 0)
{
return;
}
int j = 0 ;
int n = size;
Boolean flag = TRUE;
while(flag)
{
flag = FALSE;
for(j = 1; j < n; j++)
{
if(a[j-1] > a[j])
{
Swap(&a[j-1], &a[j]);
flag = TRUE;
}
}
n--;
}
}
|
进一步优化,可以一个标记flag来表示当前的状态,在每轮比较的开始把flag置为0,则代表没有发生排序,如果发生了排序,则把flag值为1,在下次的循环中继续进行比较。
如果有100个数的数组,仅前面10个无序,后面90个都已排好序且都大于前面10个数字,那么在第一趟遍历后,最后发生交换的位置必定小于10,且这个位置之后的数据必定已经有序了,记录下这位置,第二次只要从数组头部遍历到这个位置就可以了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void BubbleSort3(int *a, int size)
{
if(NULL == a || size < 0)
{
return;
}
int j = 0 ;
int n = size;
int flag = n;
while(flag > 0)
{
n = flag;
flag = 0;
for(j = 1; j < n; j++)
{
if(a[j-1] > a[j])
{
Swap(&a[j-1], &a[j]);
flag = j;
}
}
}
}
|

功能检测
- 检测代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int main()
{
int i =0;
int a[] = {3,0,1,8,7,2,5,4,6,9};
int n = sizeof(a)/sizeof(a[0]);
BubbleSort1(a, n);
printf("\n");
for(i = 0; i < n ; ++i)
{
printf("%3d",a[i]);
}
printf("\n");
return 0;
}
|
- 运行结果:
1
2
3
4
5
6
7
8
| root@aemonair:~/Desktop# cc.sh BubbleSort.c
Compiling ...
-e CC BubbleSort.c -g -lpthread
-e Completed .
-e Sat Jul 23 18:42:01 CST 2016
root@aemonair:~/Desktop# ./BubbleSort
0 1 2 3 4 5 6 7 8 9
|
冒泡排序毕竟是一种效率低下的排序方法,在数据规模很小时,可以采用。数据规模比较大时,最好用其它排序方法。